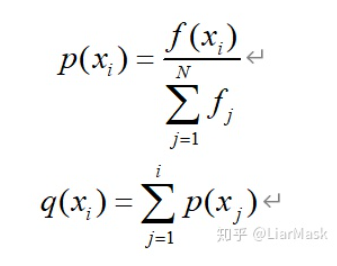• Q-learning 算法
  是强化学习的一种方法。Q-学习就是要记录下学习过的策略，因而告诉智能体什么情况下采取什么行动会有最大的奖励值。Q-学习不需要对环境进行建模，即使是对带有随机因素的转移函数或者奖励函数也不需要进行特别的改动就可以进行。
  对于任何有限的马可夫决策过程（FMDP），Q-学习可以找到一个可以最大化所有步骤的奖励期望的策略。在给定一个部分随机的策略和无限的探索时间，Q-学习可以给出一个最佳的动作选择策略。
  “Q”这个字母在强化学习中表示一个动作的期望奖励。
  
• 遗传算法
  是计算数学中用于解决最优化的搜索算法，是进化算法的一种。
  遗传算法通常实现方式为一种计算机模拟。对于一个最优化问题，一定数量的候选解（称为个体）可抽象表示为染色体，使种群向更好的解进化。传统上，解用二进制表示（即0和1的串），但也可以用其他表示方法。进化从完全随机个体的种群开始，之后一代一代发生。在每一代中评价整个种群的适应度，从当前种群中随机地选择多个个体（基于它们的适应度），通过自然选择和突变产生新的生命种群，该种群在算法的下一次迭代中成为当前种群。
  • 精英保留
    遗传算法(Genetic Algorithm)中的基因，并不一定真实地反映了待求解问题的本质，因此各个基因之间未必就相互独立，如果只是简单地进行杂交，很可能把较好的组合给破坏了，这样就没有达到累积较好基因的目的，反而把原本很好的基因给破坏了。精英保留策略可以避免最优个体不会因为杂交操作而被破坏。
    “精英保留”(maintain the best solution found over time before selection)策略是De Jong针对遗传算法提出来的。对遗传算法来说，能否收敛到全局最优解是其首要问题。
  • 轮盘赌
    轮盘赌选择法（roulette wheel selection）是最简单也是最常用的选择方法，在该方法中，各个个体的选择概率和其适应度值成比例，适应度越大，选中概率也越大。但实际在进行轮盘赌选择时个体的选择往往不是依据个体的选择概率，而是根据“累积概率”来进行选择。
    操作过程：
    以一个实例来讲述轮盘赌选择法的具体过程，现有一个抽奖轮盘如下：
    
    显然，当我们直接转动轮盘时抽到“参与奖”的概率最大，因为它占总体的比例最高，这也体现了“轮盘赌选择法”中所占比例越大被选中概率越高的思想。但我们一般不采用抽中“几等奖”的概率这种定性的指标来表述每个部分被选中的概率，而是引入“适应度”与“累积概率”的概念，其中每个部分被选中的概率与其适应度值成比例。设某一部分x(i)的适应度值表示为f(xi)，该部分被选中的概率为p(xi)，累积概率为q(xi)，对应的计算公式如下：
    
    上式中的累积概率表示每个个体之前所有个体的选择概率之和，它相当于在转盘上的“跨度”，“跨度”越大越容易选到，就相当于概率论中的概率分布函数F(x)。轮盘赌选择法的过程如下：
    （1）计算每个个体的被选中概率p(xi)
    （2）计算每个部分的累积概率q(xi)
    （3）随机生成一个数组m，数组中的元素取值范围在0和1之间，并将其按从小到大的方式进行排序。若累积概率q(xi)大于数组中的元素m[i]，则个体x(i)被选中，若小于m[i]，则比较下一个个体x(i+1)直至选出一个个体为止。
    （4）若需要转中N个个体，则将步骤（3）重复N次即可
    看了上面的选择过程我们可能有这样的疑问：由于个体的选择是以“累积概率”为标准的，但一个个体的累积概率q(xi)大并不表示它的选中p(xi)也大，因为根据q(xi)的计算公式我们知道累积概率表示的是每个个体之前所有个体的选择概率之和，这难道不会导致某些个体明明选中概率很小但却因为它位置靠后而导致其累积概率很大而被选中的情况发生吗？显然这与轮盘赌选择法的初衷是矛盾的啊！
    为了验证上述情况是否会发生，以上面的“轮盘抽奖游戏”为例，给每个奖项给定一个编号，编号的数字代表了他在总体中的位置，如下：
    
    由表格可以看到：“一等奖”的选中概率最小，但却因为其编号最大导致其累积概率为1，那是否会出现一等奖百分比会被选中的事件出现呢？为了验证结果，在Matlab中进行实验。进行1000次轮盘抽奖，并记录每次抽奖的编号，得到结果如下表所示：
    
    从最终的结果可以看出，采用累积概率的方式并没有出现“抽中一等奖”事件的概率很大的结果，反而最终的结果和每个奖项的选中概率相近，这说明采用累积概率的轮盘赌选择法是切实可行的，且其选择结果误差很小。